Here's the thing... I'm an Astrophysicist. And I have a very pragmatic approach to problem solving. More of an applied math approach than theoretical. Maybe you do too?
But when I ventured into understanding post-quantum cryptography, and discovered the "new" arena of Lattice Cryptography, all the information about it was waist deep in complexity and obfuscated explanations... at least to my way of thinking. Theoretical proofs of soundness are important, but so is communicating how it works, and that latter part seems deeply buried by the community.
So I finally sat down with LWE Lattice Crypto and teased it apart, to really understand what is going on. And, in the end, it becomes really quite simple to understand.
How it Works
At the heart of Lattice Crypto is the problem: How can you determine the values for X and S in this equation, when you know K and A?
A = K*X + S
Well, you can't. This is a single equation with two unknowns. It seems to be an effective way to hide one or both of X and S - an encryption scheme, provided that you can easily reverse the encryption.
From an attacker's perspective, there are potentially any number of possible solutions. To really nail down X and S, you need another equation. But if we knew that the domain of X and S were limited, we could try a brute-force search.
Of course, LWE Lattice Crypto is more complicated than this single equation, but the problem is basically the same:
skey = [1 | x]
PKey = [b | -A]
c = Trn[PKey] • s + w * m ; this is the analog of our A = K*X + S
where,
b = A • x + ψ ; and so is this...
and where,
skey = secret key vector with 1 prepended to NCol vector of field random values, x.
PKey = public key matrix, formed by prepending the b column vector to the negated A matrix.
c = crytpotext vector with (NCol+1) elements
b = vector with NRow elements
A = random matrix with NRow rows, and NCol columns, over the finite field
s = binary selection vector with NRow elements, each of which are 0 or 1
w = message bit weighting = Floor(p/2)
p = prime modulus of finite field
m = bit message with NRow elements, = [bit, 0, 0, ... , 0] for bit = 0 or 1.
x = random secret key vector with NCol elements over the finite field
ψ = sampled Gaussian noise vector with NRow elements, over the domain of the finite field, with zero mean, and variance chosen so that:
Prob(|Trn[ψ] • s| < Floor(p/4)) = (1 - ε), for vanishingly small ε.
We can rewrite the cyrptotext vector, c, as:
c = Trn[PKey] • s + w * m
= Trn[b | -A] • s + w * m
= [Trn[b] • s + w * bit | Trn[-A] • s]
writing the vector as a scalar prepended to a subvector.
Decryption is by way of forming the vector dot-product between the secret key and the cryptotext vector:
Trn[skey] • c = Trn[1 | x] • [Trn[b] • s + w * bit | Trn[-A] • s]
= Trn[b] • s + w * bit - Trn[x] • Trn[A] • s
= Trn[x] • Trn[A] • s + Trn[ψ] • s + w * bit - Trn[x] • Trn[A] • s
= Trn[ψ] • s + w * bit
Then, by rescaling this by 1/w, and then rounding its value to the range (-1, 1), the bit is recovered by taking that rounding as an element of the finite field with modulus 2.
The additive Gaussian noise vector, ψ, smears out the encoding so that the decryption dot product produces a value in the range of (-p/4, p/4), if the bit were 0, or else (-3 p/4, -p/4) or (p/4, 3 p/4) if the bit were 1. Rescaling by 1/(p/2) produces a range (-1/2, 1/2) for bit 0, or else (-1, -1/2) or (1/2, 1) for bit 1.
But notice that, depending on the variance of the underlying noise distribution for ψ, we may have a probabilistic decryption. Some decrypting errors become possible.
But ultimately, encryption is a situation like A = K*X + S, where only A and K are known, but having many more dimensions.
Making It Fortified
You hide your secret keying, the random x vector, by adding noise, ψ, and stating NRow equations, the b vector, in (NRow + NCol) variables. In this case we always have more variables than equations. Variables in x and ψ vectors range over the finite field. A brute force attack could be mounted, so you want to make that infeasible by choosing a large enough domain and large enough values for NRow and NCol.
And you hide the data being encrypted, which produces (NCol+1) equations, the c cryptotext vector, in (NRow+1) variables, the s selection vector and the message bit, by ensuring that NRow > NCol. But in this case, the s elements and bit are known to be either 0 or 1. So a brute force search could be more easily mounted. So you make sure things remain hidden by choosing sufficiently large values for NRow and NCol, which produces a brute-force search problem of O(2^(NRow+1)).
Chosen plaintext attacks are thwarted by using a fresh random binary selection vector, s, for each bit being encrypted. Any two collections of encryptions of the same multi-bit message are highly unlikely to contain the same cryptotext vectors in the same sequence. Even for encryption of only one bit, the probability of producing the same cryptotext vector is 1/2^NRow.
From a physicist's perspective, the fundamental indeterminacy has nothing to do with shortest-vector problems over a finite-field lattice. It stems from some fundamental theorem of basic algebra. Finite fields aren't even required. (see below) If you have N equations in M unknowns, and N < M, then you cannot uniquely solve for the unknowns.
But brute-force searching is always a possibility. So let's put some numbers in for showing degrees of difficulty for brute-force searches.
A Concrete Example
Let's say we choose arithmetic over a finite field with a prime modulus, say p = 2^30 - 35. That's 30 bits. And suppose we make NRow = 320, and NCol = 256. This satisfies the condition that NRow > NCol. The other condition, NRow < (NRow + NCol), is always trivially satisfied.
Then for attacking the secret keying, we only need to examine the published public key matrix. The equations for the random x vector and noise vector elements, come from examining the b vector and A matrix. With 320 noise values, 256 random x values, each at 30 bits per element, the correct solution is some specific 30*(256+320) = 17280 bit key! That's a mighty big key-space to search.
Now for attacking the encryption, attempting to discover the 1-bit message being transmitted by the cryptotext vector, we know that the 320 selection weights are all either 0 or 1, and the bit being sent is either 0 or 1. So in this case we have 2^321 possible keyings. That's still a decently enormous key-space to search. And these weights all change to new random 0 and 1 values for every message bit being encrypted for transfer.
Yes, you heard it right - I have mentioned, multiple times, that the encryption applies to a single bit of message. If you want to send a 256-bit message you need to produce 256 separate encryptions. Each encryption will use a different random selection vector, s. And each of those encryptions will produce a 257 element vector of 30-bit numbers as a cryptotext vector.
So, while Lattice Crypto may be uncrackable, even for quantum computers, it is really inefficient for data transmission. At most, you would probably only use Lattice Crypto to securely transfer a shared secret key, and then use that key for something more efficient, like AES-256 encryption, for the rest of the message. Transmitting that secret key will require the sending of 256*257 = 65,792 30-bit numbers. That's a lot of network traffic for a mere 256 bits of keying.
So What Is Really Going On Here?
After wading through all the symbolic math, we have to pull back and think about it from a distance. Let's first tackle the b vector.
The elements of the b vector are simply an ordered collection of vector dot-products between a secret x vector and a bunch of random vectors that lie in the same hyperspace as the x vector. Then some scaled random noise is added with the ψ vector. The A matrix contains those random vectors as its rows.
Just imagine holding a bunch of ball bearings in your hand and dropping them all at once on the ground. They land in any random variety of positions. Choose a vacant location somewhere among the ball bearings for a coordinate system origin, and draw rays from that origin to each ball bearing.
Now pick one of those rays as a secret x vector. Create the A matrix as an ordered collection of the remaining ray vectors. Then the b vector is simply the ordered list of the vector dot-product between the x vector and all the other rays gathered up in the A matrix. Then add some scaled noise to every element of that b vector.
Of course, we need to be thinking about doing this in a high-dimensional hyperspace, instead of using a 3-dimensional bunch of ball bearings, dropping them onto a 2-dimensional surface. But, seen from this perspective, it becomes obvious that it doesn't matter where any of the ball bearings land, nor if several of them lie along the same ray from the origin. There is no concern about degenerate subspaces represented in the A matrix. None of the hi-falutin linear algebra stuff. We will never need to invert the A matrix. We only need to use it when encrypting a message.
All we need to do is record how similar the ray vectors are to the chosen x vector, using the vector dot-product as that measure, then add a little noise. The added noise ensures that all the measurements are perturbed away from their actual dot-product. Not only does nobody know the angles between the ray vectors and the secret x vector, but they don't even know how long the x vector is, i.e., how far from the origin that ball bearing landed. And they certainly don't know by exactly how much the added noise has changed the actual measure.
It is impossible to solve any NCol equations for the secret x vector components. And to thwart brute-force attacks, just be sure to use a high dimensional space (many x vector components, NCol), and use many more ball bearings, NRow, than the dimensionality of the hyperspace, NRow > NCol.
Now, to encrypt a message bit, simply choose some subset of the b vector and sum them, along with the scaled bit value. That becomes the first element of the cryptotext c vector. Then the remaining elements of the c vector is the negated sum of the same corresponding ray vectors among the subset selection, taken from the A matrix.
Every cryptotext vector contains within it all the items needed to recover the message bit, if you know the secret x vector. The first element has the summed noisy vector dot-products between the secret x vector and the selected ray vectors, plus the scaled message bit. The remainder of the c vector contains the negated summed ray vectors used to form that b sum in the first element, sitting ready for a vector dot-product with the secret x vector: the dot-product with a sum of vectors is the same as the sum of the dot-products with each vector.
But to the outside world, who does not know the x vector, this just looks like a jumble of numbers. Sure they know that the second through last elements of the c vector are a sum of elemental ray vectors, all easily gleaned from the -A matrix portion of the public PKey matrix.
But this becomes a complicated Subset Sum Problem - exactly which ray vectors were used to form that sum vector? That is an unwieldy combinatorial problem. So the random subset selection process remains hidden by the difficulty of that problem.
And too, if one could tease out the selector vector, s, then they might be able to use the stated b vector, the first column of the public PKey matrix, to help uncover the concealed message bit contained in the first element of the c vector. So keep the random subset selector vector large (NRow) to make the problem as difficult as possible.
In practice, nobody knows the subset selection vector used during encryption. The encryptor simply generates a non-null random binary vector for each message bit encryption, then promptly forgets it. The owner of the secret x vector doesn't care, since all the information they need, to back out its contribution to the first element of the cryptotext vector, is present in the remaining elements of the c vector. We're making the recipient of the cryptotext act as our mule, to help us when we need to decrypt the message bit.
The encryption process is really quite simple. It is almost as though we are hiding the message bit in plain sight. But not quite... It really is a case of knowing A and K, but not X and S, in our equation:
A = K*X + S.
But, Wait a Minute!
We know the dimensionality of the secret key vector, x. It is the same as the length, less one, of any cryptotext vector. In fact it is the same as the row-length of the A matrix planted prominently in the published PKey matrix.
And since NRow > NCol, we should be able to pick any NCol subset of those vectors and reframe the problem in terms of orthogonal basis vectors spanning the same space. We ought to be able to tease apart the problem and recover the hidden x vector.
Surely, not all of the ball bearings fell along the same ray vector. There must be some NCol collection of ray vectors that could also serve as non-orthogonal basis vectors spanning the subspace. It is easy enough to check. Just form the Determinant of the selected A matrix row vectors. If it is non-zero, then we have a spanning collection. You might have to try a few different collections before you find it. But if NCol is large, and NRow is larger, then we have a fighting chance.
So, now... we have a system of NCol equations in, uh oh, 2*NCol unknowns... But we do know something about those added noise dithers, meant to throw us off. We know that they are such that any subset sum of them, and hence, any one of them, are likely in the range (-p/4, p/4). Can this be considered a small perturbation?
It is at this point, where the Shortest Vector Problem Over a Lattice, and Learning With Errors (LWE), shows up. Can we solve a system of equations, with added noise, to find the underlying unknowns? The claim is that attempting to use Gaussian Elimination, in the presence of noise, amplifies the noise to such an extent that it begins to hide the unknowns, erasing knowledge. And how do you solve a system over a finite field anyway? Chinese Remainder Theorem? Uh oh...
So try using Graham-Schmidt Orthogonalization, and avoid the scaled summing of Gaussian Elimination. What then?
It is at this point that I will take my bow, and exit like any self-respecting Astrophysicist, and simply posit that the geniuses in the community have deemed this a difficult enough problem that, by adding the noise as specified, we substantially increase the difficulty over high dimensional spaces, to the point where we can feel confident about our secrets remaining hidden. I know... a cheap exit. But hey, I just wanted to understand how it works, not furnish retreaded proofs of security.
But if this is true, then maybe we don't need to be so restrictive about the relative size of NRow vs NCol? I don't know. But I do know that the algebra states that you can't find NRow unknowns from NCol equations when NRow > NCol. So I will live by that for the moment.
The Arithmetic of Lattice Crypto
Now notice that the equations are true for any self-consistent arithmetic. To prove a point, I verified that they work just fine to encrypt and decrypt a bit, using floating point arithmetic over the Reals. (See the Appendix) I used random values from a zero mean, unit variance, Gaussian distribution. The message bit had unit weight.
You don't have to use finite field arithmetic. And you don't even have to use Gaussian randomness. The sums in the b vector will tend toward Gaussian anyway, thanks to the Central Limit Theorem.
But using finite field arithmetic also works, and it does a better job than floating point Real arithmetic in terms of hiding patterns in the resulting encryptions.
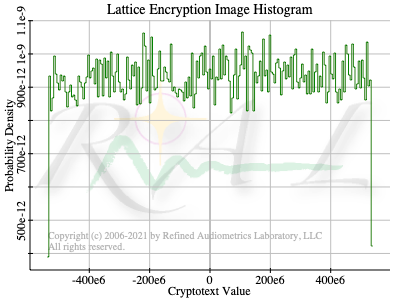
An image created by performing 256 floating-point encryptions, and laying out the rows of each encryption beneath one another, showed a strong random vertical stripe coming from the first element of the cryptotext vectors and weaker uniform noise elsewhere. But when using finite field arithmetic, the image was uniformly random salt & pepper noise. (See Appendix Image and Histograms)
That stripe (first element) corresponds to the values of the b vector and the added bit value. The stripe is the only value in the cyphertext vector that contains the message bit. The bit value, either 0.0 or 1.0, was completely swamped by large absolute values, being in the general range of 12.0 to 500.0.
A histogram of a floating-point block encryption showed an, essentially zero mean, Gaussian distribution of values with large, rare, outlier values, whereas a finite-field block encryption showed a uniform noise distribution, and of course, all values lay within the modular field.
Whether these patterns have any significance or not is an open question. I doubt they do. I could not visually discern any correlation of the stripe values with the bit value being encrypted. The summed weighted randomness of the x vector multiplied by the randomness of the A matrix, then summed by the random selection vector, buries the message bit value deep beneath the noise level. The additive noise vector, ψ, has almost no discernible effect.
Could there be some weak correlation? I would expect to see the bit value riding about 27 to 52 dB, on average about 40 dB, below the noise. It is 0.0 or 1.0 atop a near Gaussian distribution with zero mean and a standard deviation of, randomly, 23 to 400.
Experimentally, from observing multiple runs of encrypting 256 bits, I observe that the standard deviation of the stripe is around 140. That puts the bit value at 42 dB below the noise level. Could you detect the bit with only a single look? I doubt it. Your confidence would be exceedingly low. Any determination would be very nearly 50/50 for being correct. No better than random chance.
So all that the stripe shows is an exaggerated (scaled) average value for the cross correlation between the secret key and the A matrix rows. The other, off-stripe, values simply show the scaled average value of the A matrix rows. Which rows contribute to these averages is controlled by the random selection vector. The stripe shows sums of products, while the off-stripe region shows simple sums.
But, amazingly, in the face of all this huge random noise, the arithmetic of the equations is correct, and forming the vector dot-product between the secret key and a cryptotext vector reliably produces values that round properly to recover the encrypted bit. The lion's share of the noise is exactly trimmed away by use of the proper secret key, to reveal the bit value plus a small fuzzball of noise. The arithmetic is precise enough in single-precision floating-point, to preserve the boundary of the additive Gaussian masker noise. Bits are faithfully recovered.
Also, note that while the lattice crypto community seems fond of using prime modulus finite field arithmetic, but modified to work with values in the range (-p/2, p/2), instead of [0, p), this really isn't necessary. Using plain old modular arithmetic works just as well. (It is modular after all...)
Noise Scaling
A variation on the theme provides for using additive Gaussian noise with some fixed scaling, for the elements of the ψ vector. But sometimes, when a variate has large deviation, this can produce an incorrectly recovered bit during decryption.
So long as the scaling of the noise is sufficient to make this a rare occurrence, we can still recover groups of encrypted bits by using Hamming (4,7) encoding. We translate the message bytes into 4-bit nibbles, transmitted as 7 bits of Hamming code. On reading back 7 successive encryptions, decrypting and performing Hamming Error Correction, we can reliably recover the transmitted nibble, in the face of infrequent soft errors.
But this nearly doubles the encryption load, and cannot guarantee freedom from hard decoding errors. So, instead, by carefully choosing the additive noise scaling to guarantee worst case behavior below the necessary threshold, we can avoid the need for this Hamming ECC, have guaranteed decryption reliability, and keep the encryption to more reasonable, albeit still large, amounts.
The choice of noise scaling occurs when the public key is constructed. A single ψ vector is generated. We can separately gauge the impact of a selection vector choosing all the positive deviates, or all of the negative deviates. Whichever sums greater in absolute value dictates how much scaling the public key noise will need, to provide decryption guarantees. This noise level might sometimes provide a small amount less masking than when using some fixed fraction with attendant Hamming ECC.
Keying
Unlike most public key cryptosystems, Lattice Crypto allows for the generation of any number of different public keys, all corresponding to one secret key. Public keys can be configured with different random A matrices and different random noise vectors, ψ. But only the holder of a secret key can produce a public key.
Wondering about the possible utility from using different public keys, but there really isn't any way to distinguish cryptotext vectors as having come from one public key or another, unless the A matrix were designed more like an identity matrix. But doing that would give away information about the underlying secret key and the encrypted bit of a message.
So, for now, this just seems a curious property of Lattice Crypto. Apart from different noise scaling in the ψ vector, one batch of randomness seems about as good as any other.
Summary
Lattice Crypto is a linear system. It works by using fundamental theorems of algebra, in that you can't solve a system of equations in more variables than equations, and it thwarts brute force attacks by using very large key-spaces.
So analytic cracking is impossible, and brute force attacks are infeasible. There are no underlying periodicities to provide an advantage for quantum computing.
It appears that the weakest aspect of Lattice Crypto may lie in the quality of randomness. There may also be some requirement on the minimum level of masking noise employed.
 |
| FLattice Image |
 |
| Finite Field Lattice Image |